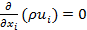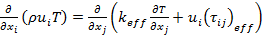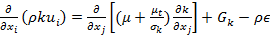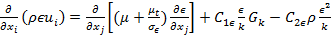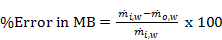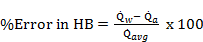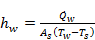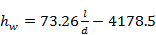Volume 2 - Year 2014 - Pages 33-42
DOI: 10.11159/ijmem.2014.004
Effect of Channel Size on Heat Transfer and Pressure Drop in Thin Slabs Minichannel Heat Exchanger
Mohammed Ismail, Shahram Fotowat, Amir Fartaj
University of Windsor 401 Sunset Avenue, Windsor, Canada
ismailf@uwindsor.ca; fotowat@uwindsor.ca; fartaj@uwindsor.ca
Abstract - The effect of circular channel diameter on convective heat transfer and pressure drop behaviors in thin slabs minichannel heat exchanger is studied using a three-dimensional computational fluid dynamics (CFD) modeling. De-ionized water and air are considered as working fluids and aluminum as slab material for the particular interest of the current study. In this study, four different channel diameters of 0.25, 0.5, 0.75, and 1 mm are considered. Investigation is evaluated for the liquid side Reynolds number of 100, 400, 700, 1000, and 1300. The simulations are performed with parallel processing of 8 CPUs using a finite volume method based commercial CFD code. Three-dimensional double precision pressure-based absolute velocity formulation with parallel processing is employed. The constant temperature of 76° for water inlet and 14° for air inlet are considered for all cases in this study. The effects of channel diameter over liquid-side temperature drop, heat transfer coefficient, pressure drop, and Nusselt number are analyzed and reported in this paper. Results show that the changes in the pressure drop decreases with increasing channel diameter and decreasing Reynolds number; however, for higher diameter and lower Reynolds number, it is found to be negligible. For a constant Reynolds number, the heat transfer coefficient of water increases and the Nusselt number decreases with the increase of l/d. However, the Nusselt number of water is observed to be higher than that of the theoretical prediction because the flow in the current study is neither hydrodynamically nor thermally fully developed before the entrance and through most of the channel length.
Keywords: Channel diameter, simulation, heat transfer, thin slab, minichannel heat exchanger.
© Copyright 2014 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2013-09-20
Date Accepted: 2014-02-23
Date Published: 2014-07-07
Nomenclature
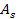 : Heat transfer surface area,
: Heat transfer surface area, 
 : Constant
: Constant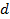 : Channel inside diameter,
: Channel inside diameter, 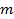
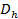 : Hydraulic diameter,
: Hydraulic diameter, 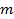
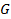 : Constant
: Constant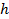 : Heat transfer coefficient,
: Heat transfer coefficient, 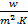
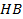 : Heat
balance
: Heat
balance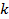 : Thermal conductivity,
: Thermal conductivity, 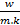
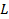 : Channel
length,
: Channel
length, 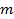
- l: Slab
length,
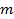
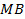 : Mass
balance
: Mass
balance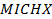 : Minichannel
heat exchanger
: Minichannel
heat exchanger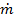 : Mass flow rate,
: Mass flow rate, 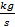
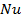 : Nusselt number
: Nusselt number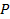 : Pressure,
: Pressure, 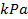
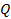 : Heat
transfer rate,
: Heat
transfer rate, 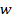
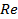 : Reynolds number
: Reynolds number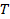 : Temperature,
: Temperature, 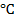
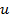 : Velocity,
: Velocity,
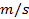
Greek Symbols
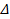 : Difference
: Difference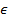 : Rate of turbulence kinetic energy dissipation,
: Rate of turbulence kinetic energy dissipation, 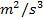
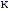 : Turbulence kinetic energy, m² /s²
: Turbulence kinetic energy, m² /s²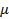 : Dynamic
viscosity,
: Dynamic
viscosity, 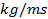
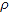 : Density, kg/m³
: Density, kg/m³
Subscripts
 : Airside
: Airside 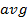 : Average
: Average 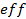 : Effective
: Effective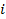 : Inlet
: Inlet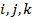 : Components
in x, y, and z directions respectively
: Components
in x, y, and z directions respectively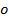 : Outlet
: Outlet : Surface
: Surface : Turbulent
: Turbulent : Deionized water
: Deionized water
1. Introduction
Several
studies dealing with the single-phase forced convection heat transfer in micro
devices have been printed in previous years, owing to the rapid development of micro-electromechanical
devices during the last decade. This growth has great influence on micro scale devices,
including microelectronic cooling systems and micro heat exchangers. Single-phase
heat transfer coefficients in six rectangular channels with a hydraulic
diameter (![]() ) of 0.31 to 0.75
) of 0.31 to 0.75 ![]() for water and methanol were
reported by Wang and Peng [1]. Their Nusselt numbers (
for water and methanol were
reported by Wang and Peng [1]. Their Nusselt numbers (![]() ) were only 35% of that
predicted by Dittus-Boetler [2] equation. However, Webb and Zhang [3] discussed
the capability of commonly accepted correlations to predict single-phase and
two-phase heat transfer and friction in channels with small hydraulic diameters
between 0.1 mm and 2.0 mm. They found that their experimental results were
adequately predicted by the established correlations for single-phase flow in
multiple tubes with
) were only 35% of that
predicted by Dittus-Boetler [2] equation. However, Webb and Zhang [3] discussed
the capability of commonly accepted correlations to predict single-phase and
two-phase heat transfer and friction in channels with small hydraulic diameters
between 0.1 mm and 2.0 mm. They found that their experimental results were
adequately predicted by the established correlations for single-phase flow in
multiple tubes with ![]() .
.
The
flow and heat transfer characteristics for the run of nitrogen gas in heat
exchangers were measured by Wu and Little [4]. They found that for laminar flow
with a Reynolds number (![]() ) of less than 600,
) of less than 600, ![]() was lower than those
predicted by traditional correlations, whereas for
was lower than those
predicted by traditional correlations, whereas for ![]() ,
, ![]() was higher than the
standard values. Several effects that are neglected when considering macro
scale flow were identified by Papautsky et al. [5]. For example, micro scale
phenomena may include two- or three-dimensional transport effects, and the
temperature dependent variations of the transport fluid properties along a
microchannel may invalidate the often used assumption of constant properties,
so that to provide conclusive evidence of micro scale effects, amended
measurement accuracies are required.
was higher than the
standard values. Several effects that are neglected when considering macro
scale flow were identified by Papautsky et al. [5]. For example, micro scale
phenomena may include two- or three-dimensional transport effects, and the
temperature dependent variations of the transport fluid properties along a
microchannel may invalidate the often used assumption of constant properties,
so that to provide conclusive evidence of micro scale effects, amended
measurement accuracies are required.
The
liquid flow friction factor and heat transfer coefficient in circular and
rectangular mini-channels with hydraulic diameters of 0.77 to 2.01 ![]() were quantified by
Agostini et al. [6]. They found good agreement between their experimental
results in the turbulent regime and the Gnielinski [7] correlation. Conversely,
in the laminar regime, no precise prediction was found, and most of the heat
transfer test results were expressively divergent from those predicted by the
traditional forced convection heat transfer correlations. However, three main
causes were explained for the differences between the experimental results
obtained in minichannel heat exchanger compared to macro-tubes: uncertainties
on the channel dimensions, inlet and outlet singular pressure losses, and
longitudinal heat conduction. Good agreement was found with standard
correlations and theories, while these elements are taken into account.
were quantified by
Agostini et al. [6]. They found good agreement between their experimental
results in the turbulent regime and the Gnielinski [7] correlation. Conversely,
in the laminar regime, no precise prediction was found, and most of the heat
transfer test results were expressively divergent from those predicted by the
traditional forced convection heat transfer correlations. However, three main
causes were explained for the differences between the experimental results
obtained in minichannel heat exchanger compared to macro-tubes: uncertainties
on the channel dimensions, inlet and outlet singular pressure losses, and
longitudinal heat conduction. Good agreement was found with standard
correlations and theories, while these elements are taken into account.
Experimental
and numerical studies were conducted by Li et al. [8] to characterise the flow
and heat transfer behaviors of liquid laminar flow in microtubes. The smooth
fused silica and rough stainless steel microtubes were used with hydraulic
diameters of 50–100 ![]() and 373–1570
and 373–1570![]() , respectively. The
experiment was conducted with deionized water at the Reynolds number from 20 to
2400. They established that the experimental results of local Nusselt number
distribution along the axial direction of the stainless steel tubes did not
comply with the conventional results when Reynolds number was low and the
relative thickness of the tube wall was high. The numerical study revealed that
the large ratio of wall thickness over tube diameter in low Reynolds number
region causes significant axial heat conduction in the tube wall, leading to a
non-linear distribution of the fluid temperature along the axial direction. The
axial heat conduction effect was gradually weakened with the increase of
Reynolds number and the decrease of the relative tube wall thickness.
, respectively. The
experiment was conducted with deionized water at the Reynolds number from 20 to
2400. They established that the experimental results of local Nusselt number
distribution along the axial direction of the stainless steel tubes did not
comply with the conventional results when Reynolds number was low and the
relative thickness of the tube wall was high. The numerical study revealed that
the large ratio of wall thickness over tube diameter in low Reynolds number
region causes significant axial heat conduction in the tube wall, leading to a
non-linear distribution of the fluid temperature along the axial direction. The
axial heat conduction effect was gradually weakened with the increase of
Reynolds number and the decrease of the relative tube wall thickness.
Harirchian
and Garimella [9] experimentally investigated the effects of channel size, heat
flux, and mass flux (225-1420 ![]() ) on flow boiling
regimes in mini and micro-channels flow boiling regimes using high speed
photography. Seven dissimilar silicon test pieces with a depth of 400
) on flow boiling
regimes in mini and micro-channels flow boiling regimes using high speed
photography. Seven dissimilar silicon test pieces with a depth of 400 ![]() with parallel channels
widths from100 to 5850
with parallel channels
widths from100 to 5850 ![]() are used. The picturing
and the heat transfer data show that nucleate boiling is dominant, flow regimes
are similar in the channels of width 400
are used. The picturing
and the heat transfer data show that nucleate boiling is dominant, flow regimes
are similar in the channels of width 400 ![]() and large and differ
from 100-250
and large and differ
from 100-250 ![]() wide channels, over a
wide range of heat flux. It is also stated that with increase of channel width,
bubbly flow substitutes slug flow and intermittent churn/wispy-annular flow
substitutes intermittent churn/annular flow. It is established that for channels
width of 400
wide channels, over a
wide range of heat flux. It is also stated that with increase of channel width,
bubbly flow substitutes slug flow and intermittent churn/wispy-annular flow
substitutes intermittent churn/annular flow. It is established that for channels
width of 400 ![]() and larger, for the
range of heat fluxes in which nucleate boiling occurs on the channel walls, the
heat transfer coefficient is independent of mass flux regardless of the flow
pattern.
and larger, for the
range of heat fluxes in which nucleate boiling occurs on the channel walls, the
heat transfer coefficient is independent of mass flux regardless of the flow
pattern.
The various mechanisms for the departure of flow and heat transfer correlations for flow in microchannels from the standard ones were categorized into two groups by Guo and Li [10]. First, if the characteristic length of the flow and the molecular mean free path are on the same order of the magnitude, the Navier-Stokes equations and the Fourier heat conduction equation failure, and accordingly, the flow and heat transfer behaviours change significantly. This is the so-called rarefaction effect which can be shown by the Knudsen number, expressed by the ratio of the molecular mean free path and the characteristic length of the flow. Secondly, the size effect on the flow and heat transfer correlations is attributed to the disparity of the governing factors in the flow and heat transfer as the scale decreases even if the continuum assumption is still applicable. For example, forces employed on the fluid that affect the flow and heat transfer whose result on the convection changes at different scales, and also axial heat conduction in the tube wall, which are usually neglected for normal-sized devices, may become significant on a micro scale. Consequently, micro scale flow and heat transfer correlations vary from those of normal-sized devices.
The
experiment of water flow in circular microtubes of fused silica and stainless
steel with the hydraulic diameter of 50 to 254 ![]() was executed by Mala
and Li [11]. The mean surface roughness of the tubes was ±1.75
was executed by Mala
and Li [11]. The mean surface roughness of the tubes was ±1.75 ![]() , and the relative
roughness of the tubes with
, and the relative
roughness of the tubes with ![]() and
and ![]() was from 1.36% to 1.70%
respectively. They noted that for low
was from 1.36% to 1.70%
respectively. They noted that for low ![]() , there is a nonlinear
trend between pressure drop and flow rate, and the friction factors were
steadily higher than those predicted by standard correlations. The authors
predicted the transition from laminar to turbulent flow at
, there is a nonlinear
trend between pressure drop and flow rate, and the friction factors were
steadily higher than those predicted by standard correlations. The authors
predicted the transition from laminar to turbulent flow at ![]() , and the fully
developed turbulent flow at
, and the fully
developed turbulent flow at ![]() due to the effect of
the surface roughness of the microtubes. Lelea et al. [12] experimentally and
numerically studied developing and laminar flow regime for distilled water as
the working fluid and stainless steel as the tube material with Reynolds number
range up to 800 in microtubes with diameter of 0.1, 0.3, and 0.5
due to the effect of
the surface roughness of the microtubes. Lelea et al. [12] experimentally and
numerically studied developing and laminar flow regime for distilled water as
the working fluid and stainless steel as the tube material with Reynolds number
range up to 800 in microtubes with diameter of 0.1, 0.3, and 0.5 ![]() . They designed the
experimental setup such a way to facilitate the study of friction factor and
developing heat transfer. The experimental results have been compared both with
numerical and theoretical predictions from literature for conventional tubes.
It is stated that the conventional theories are valid for water flow through
microtubes obtained by numerical modeling of their experiment.
. They designed the
experimental setup such a way to facilitate the study of friction factor and
developing heat transfer. The experimental results have been compared both with
numerical and theoretical predictions from literature for conventional tubes.
It is stated that the conventional theories are valid for water flow through
microtubes obtained by numerical modeling of their experiment.
The
effects of diameter on two phase pressure drop in narrow circular tubes using
air and water is investigated by Venkatesan et al. [13]. They employed the
inner diameters of 0.6, 1.2, 1.7, 2.6, and 3.4 ![]() and the superficial
velocity of 0.01–50
and the superficial
velocity of 0.01–50 ![]() and 0.01–3
and 0.01–3 ![]() for the gas and liquid
respectively. Also a high-speed CMOS camera used to visualize the two phase
flow. A correlation for predicting Chisholm parameter in slug annular flow
pattern included surface-tension effect, mass flux effect and superficial
velocities applicable for mini tubes is suggested in two-phase flow depending
on the analysis of experimental frictional pressure drop data.
for the gas and liquid
respectively. Also a high-speed CMOS camera used to visualize the two phase
flow. A correlation for predicting Chisholm parameter in slug annular flow
pattern included surface-tension effect, mass flux effect and superficial
velocities applicable for mini tubes is suggested in two-phase flow depending
on the analysis of experimental frictional pressure drop data.
Minichannel
flow passages of compact evaporators for two phase flow pattern, pressure drop
and heat transfer was studied by Kandlikar [14]. He explored an inclusive
literature review in small-diameter passages on evaporation together with some
results obtained by the author for water evaporating in 1 ![]() hydraulic diameter
multichannel passages. It is found that heat transfer rate in the minichannels
may be anticipated using the flow boiling correlations established for
large-diameter tubes, nevertheless in multichannel evaporators, it is different
from that in single-channel evaporators under the same set of operating
conditions. It is also established that the length-to-diameter ratio for
evaporators design in small-diameter channels is influenced by the heat
transfer and pressure drop characteristics.
hydraulic diameter
multichannel passages. It is found that heat transfer rate in the minichannels
may be anticipated using the flow boiling correlations established for
large-diameter tubes, nevertheless in multichannel evaporators, it is different
from that in single-channel evaporators under the same set of operating
conditions. It is also established that the length-to-diameter ratio for
evaporators design in small-diameter channels is influenced by the heat
transfer and pressure drop characteristics.
2. Numerical Methodology
In this section, the simulation method and model validation are described.
2.1. Simulation Method
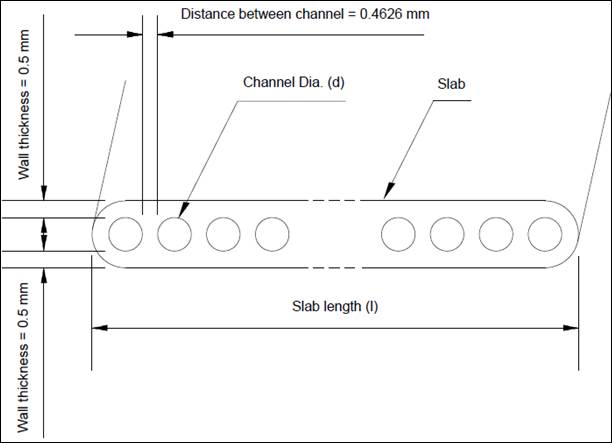
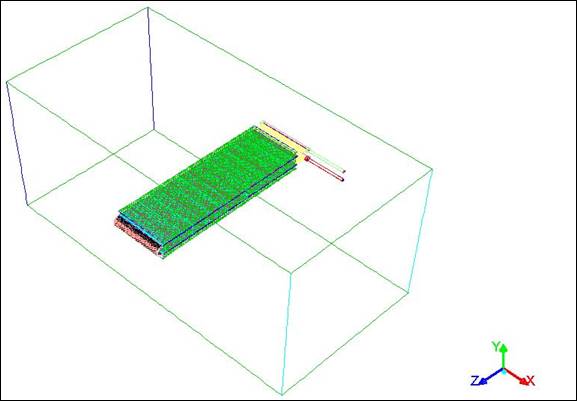
In the
current field of study, numerical modeling is performed in a multiport
serpentine slab minichannel heat exchanger (![]() ). A photograph of the
). A photograph of the ![]() , the geometry of the
slab accompanied by channels, and computational domain of the particular
interest of current research is shown in Figures 1(a)–1(d).
, the geometry of the
slab accompanied by channels, and computational domain of the particular
interest of current research is shown in Figures 1(a)–1(d).
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
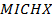 , (b) dimensions of channel
slab, (c) channels inside the thin slab with fins, and (d) computational domain
used in numerical simulations
, (b) dimensions of channel
slab, (c) channels inside the thin slab with fins, and (d) computational domain
used in numerical simulationsSpecifications of the domain extents and thin slabs minichannel heat exchanger are shown in Table 1 as follows:
Table 1. Specifications of the domain extents and channel slabs
|
Particulars |
Specifications |
|||
|
Material of the MICHX |
Aluminium alloy |
|||
|
Domain |
610mm x 305mm x 305mm |
|||
|
No. of slabs |
2 |
|||
|
No. of fins |
8 per 25.4 mm |
|||
|
Fin thickness |
0.1mm |
|||
|
Inner diameter of inlet and outlet manifold |
4.5mm |
|||
|
No. of channels inside the slab |
68 |
|||
|
Thickness of channel wall |
0.5mm |
|||
|
Channel to channel distance |
0.4626mm |
|||
|
Diameter of each channel, d |
1mm |
0.75mm |
0.5mm |
0.25mm |
|
Slab length, L |
100mm |
90mm |
66mm |
48mm |
Gambit, a code of geometry modeling, is used as a pre-processing tool to create the geometry and generate the required meshes for numerical simulation. Due to the complexity of the geometry, the whole computational domain is divided into several sub-domains, and an unstructured scheme is used to generate tetrahedral elements throughout the thermal and flow fields.
Hot de-ionized water is used as liquid-side working fluid; air flow is considered to cool the hot liquid in an across-flow orientation. ANSYS FLUENT, a widely used CFD code of finite-volume method, is used to perform the numerical simulation. A 3-dimensional, double precision, pressure-based, absolute velocity formulation with parallel processing of 8 CPUs having 64 GB of RAM is employed to perform the simulation. A standard k-ε with standard wall function turbulence model is used to solve the continuity, momentum, and energy equations to model the convective heat transfer and fluid flow process. Mass flow rates and temperature are specified for fluid inlet, pressure outlet is specified for outlet, and heat flux is specified for the adiabatic walls including inlet and outlet manifolds and serpentine of the minichannel heat exchanger in the computational set up.
In order to model the convective heat transfer process in the thin slabs minichannel heat exchanger, working fluid and flow are assumed to be steady, incompressible, and 3-dimensional. Based on these assumptions, the following simplified governing equations [15] are used to model the convective heat transfer process
|
Continuity: |
(1) |
|
Momentum: |
(2) |
|
Energy: |
(3) |
|
Turbulent Kinetic Energy, k: |
(4) |
|
Turbulent
Energy Dissipation, |
(5) |
Mass flow rates and temperature were specified for inlet working liquids, as well as inlet air. For both outlet working liquids and air, outflow boundary condition was specified. Zero heat flux is specified for test chamber and MICHX slab walls, as well as outer and inner surface at the serpentine bend. All walls are considered as stationary with no-slip conditions.
The flow of De-ionized water in the channels is considered both laminar and turbulent; whereas, the flow of air all over the MICHX test specimen is taken as turbulent only. A standard k -ε model is used to solve the turbulent flow. Initialization was computed from all-zones with a zero velocity field and run with second order upwind discretization scheme. The convergence criterion in each control volume for the flow and energy residuals are considered to be <1e-06 and <1e-10 respectively.
2. 2. Model Validation
In order to ensure that the simulation results are acceptable, the numerical verification is performed in a few ways. First, a grid dependence study is conducted to ensure that the grids are fine enough to properly capture the heat transfer and fluid flow features. Four different grid systems are conducted for this study. The grid system of about 5.5 million cells is finally considered for all cases of the numerical simulations. In this grid system, the deviations in both heat transfer rate and pressure drop are less than 3%. These errors in numerical results with compared to experimental data are acceptable for the study. Ismail et al. [15] presented the details of the grid independency, and this is not repeated here. Overall errors in mass balance (MB) and heat balance (HB) are also checked for the model. The errors in MB and HB are calculated as
|
|
(6) |
|
|
(7) |
where ![]() and
and ![]() are the mass flow rate
of water in the channel at inlet and outlet respectively;
are the mass flow rate
of water in the channel at inlet and outlet respectively; ![]() ,
, ![]() , and
, and ![]() represent water-side,
air-side, and average heat transfer rate in the system.
represent water-side,
air-side, and average heat transfer rate in the system.
The overall errors in mass and heat balance in all cases in this study are found in a very acceptable range of ±0.5% and ±3.1% respectively. The errors are shown in Figures 2(a) and 2(b).
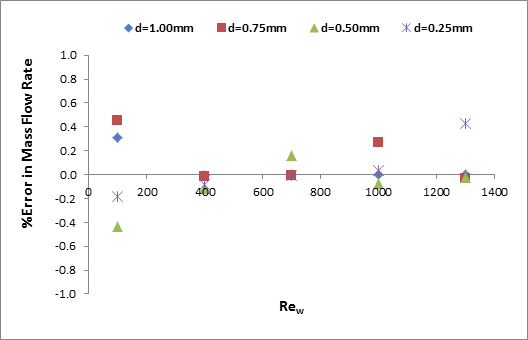
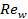
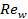
The numerical results for 1 mm channel diameter were compared with experimental results of Khan and Fartaj [16] and found to be a very good agreement. The comparison was mentioned in Ismail et al. [15] and not repeated here. Therefore, accuracy and consistency of the model used in current study may be considered as very satisfactory. Anybody can trust on the numerical results reported in this paper and can be used for investigation on the heat transfer and fluid flow characteristics in minichannel heat exchanger.
3. Results and Discussion
The sum of the normalized absolute residuals in each control volume for the flow and energy variables is considered to be less than 1e-06 and 1e-10 respectively. Simulation results are collected while the convergence is achieved below the prescribed criteria. The heat transfer-fluid flow key parameters for different channel diameters of the thin slab MICHX are reported in this section.
3. 1. The Effect of Channel Size on Water-side Temperature Drop
Channel
diameter inside the thin slabs of minichannel heat exchanger plays a
significant role in temperature drop during a cooling process. The effect of
channel diameter on water-side temperature drop, ![]() , for different Reynolds
numbers of water,
, for different Reynolds
numbers of water, ![]() is plotted in Figure 3a.
is plotted in Figure 3a.
 <
<The exit temperature of
water flow is influenced by the heat transfer mechanism between hot water and
cooled air. At a lower flow rate of water, consequently, at the lower ![]() , the fluid residence time inside the
channel is obviously more than at a higher
, the fluid residence time inside the
channel is obviously more than at a higher ![]() . Therefore, more heat transfer occurs
between two fluids, which results in the lower outlet temperature of water. The
figure also shows that for a specified
. Therefore, more heat transfer occurs
between two fluids, which results in the lower outlet temperature of water. The
figure also shows that for a specified ![]() ,
, ![]() is higher for a smaller channel
diameter.
is higher for a smaller channel
diameter.
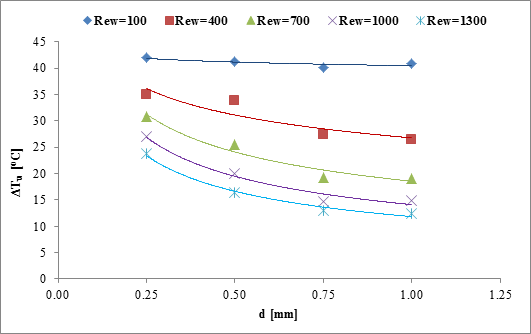
The
Effect of ![]() on water-side
temperature drop for different
on water-side
temperature drop for different ![]() is plotted in Figure 3(b).
is plotted in Figure 3(b).
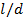 on water-side
temperature drop for different Rew
on water-side
temperature drop for different RewThe
figure shows that ![]() increases in a power law trend with the decrease
of
increases in a power law trend with the decrease
of ![]() , where
, where ![]() is the length of the
channel, and
is the length of the
channel, and ![]() is the channel
diameter. For a constant
is the channel
diameter. For a constant ![]() ,
, ![]() is higher at a higher
is higher at a higher ![]() . The material and wall thickness around
the channels are kept constant in this study. So, for the heat exchanger point
of view, the change in heat transfer is limited to the change in channel
diameter. For
. The material and wall thickness around
the channels are kept constant in this study. So, for the heat exchanger point
of view, the change in heat transfer is limited to the change in channel
diameter. For ![]() , the deviation in temperature drop due
to change in diameter, as well as l/d in the current study is found to be
negligible.
, the deviation in temperature drop due
to change in diameter, as well as l/d in the current study is found to be
negligible.
3.2. Liquid-side Heat Transfer Coefficient
The heat transfer
coefficient (![]() ), which reflects the strength of heat
convection, is a very significant parameter in heat transfer study. It is
calculated as [17]
), which reflects the strength of heat
convection, is a very significant parameter in heat transfer study. It is
calculated as [17]
|
|
(8) |
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() represent liquid-side heat transfer
rate, heat transfer surface area, liquid temperature, and inner surface
temperature of the channel respectively. The variation of heat
transfer coefficient of water with respect to
represent liquid-side heat transfer
rate, heat transfer surface area, liquid temperature, and inner surface
temperature of the channel respectively. The variation of heat
transfer coefficient of water with respect to ![]() for
for ![]() is shown in Figures 4a
and 4b.
is shown in Figures 4a
and 4b.

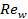
It is
apparent that for a constant ![]() , the heat transfer
coefficient of water,
, the heat transfer
coefficient of water, ![]() , increases linearly with
increases in the Reynolds number,
, increases linearly with
increases in the Reynolds number, ![]() . The slop is higher for
higher
. The slop is higher for
higher ![]() . However, for a
constant
. However, for a
constant ![]() ,
, ![]() is found to be about 3
times higher for
is found to be about 3
times higher for ![]() compared with
compared with ![]() .
.
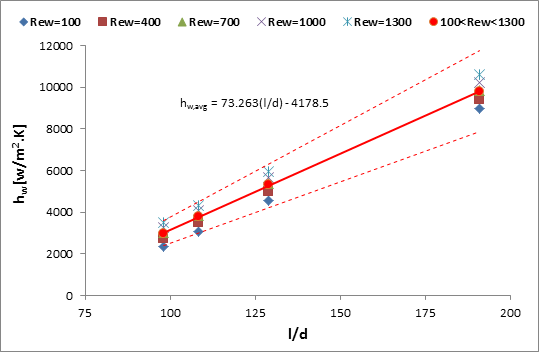
The
relationship between ![]() and the average heat
transfer coefficient of water,
and the average heat
transfer coefficient of water, ![]() , for different Reynolds
number,
, for different Reynolds
number, ![]() are shown in Figure 4b.
Within
are shown in Figure 4b.
Within ![]() 20% deviation, the
correlation is found to be
20% deviation, the
correlation is found to be
|
|
(9) |
3.. 3. Effect of Channel Diameter on Water-side Nusselt Number
The
Nusselt number (![]() ), which is the most
well-known and convenient method of representing the heat transfer, is derived
as [17]
), which is the most
well-known and convenient method of representing the heat transfer, is derived
as [17]
|
|
(10) |
where ![]() is the conductive heat
transfer coefficient of the liquid.
is the conductive heat
transfer coefficient of the liquid.
The effect
of liquid-side Reynolds number (![]() ) on Nusselt number (
) on Nusselt number (![]() ) is illustrated in Figure 6a.
) is illustrated in Figure 6a.
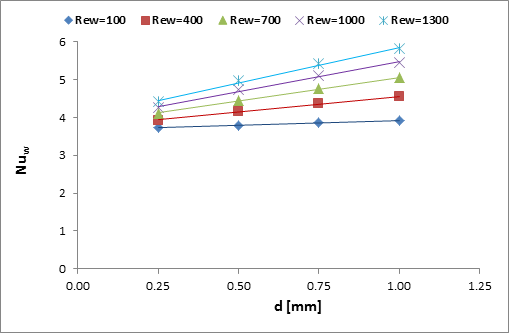
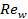
For a
constant ![]() ,
, ![]() increases with the increase
of
increases with the increase
of ![]() and the slope is
steeper for the smaller
and the slope is
steeper for the smaller ![]() . However, for a
constant
. However, for a
constant ![]() ,
, ![]() increases with the
increase of
increases with the
increase of ![]() . The relationship
between diameter and Nusselt number is best described by polynomial trend. At
Reynolds number less than 100, the channel diameter does not show significant
effect.
. The relationship
between diameter and Nusselt number is best described by polynomial trend. At
Reynolds number less than 100, the channel diameter does not show significant
effect.
The
dependency on Nusselt number (![]() ) on Reynolds number (
) on Reynolds number (![]() ) is illustrated in Figure
6b.
) is illustrated in Figure
6b.
For a
constant ![]() ,
, ![]() decreases with the
increase of channel diameter, and the slope is steeper for the smaller diameter.
However, for a constant channel diameter,
decreases with the
increase of channel diameter, and the slope is steeper for the smaller diameter.
However, for a constant channel diameter, ![]() increases with the
increase of
increases with the
increase of ![]() . For all cases, results
show the higher value for the
. For all cases, results
show the higher value for the ![]() in comparison with the
theoretical value of
in comparison with the
theoretical value of ![]() for fully developed
laminar flow at a uniform surface temperature boundary condition. The reason is
that in the current study, the flow is neither hydrodynamically nor thermally
developed. The best fit of the
for fully developed
laminar flow at a uniform surface temperature boundary condition. The reason is
that in the current study, the flow is neither hydrodynamically nor thermally
developed. The best fit of the ![]() with the
with the ![]() follows polynomial trend. However, it is observed that for Reynolds
number of 100, Nusselt number becomes close to 3.66 regardless of the channel
diameter.
follows polynomial trend. However, it is observed that for Reynolds
number of 100, Nusselt number becomes close to 3.66 regardless of the channel
diameter.
In Figure
6c, the water-side Nusselt number is evaluated against ![]() for
for ![]() .
.
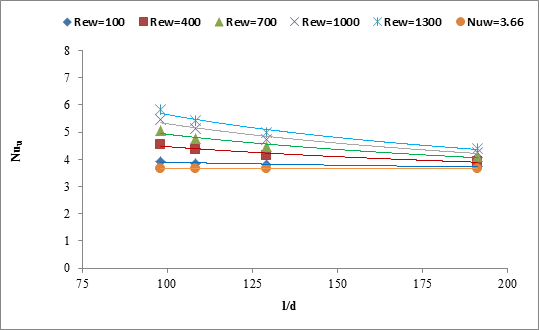
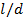 on the water-side Nusselt number for different Reynolds number
on the water-side Nusselt number for different Reynolds numberIt
is obvious from the figure that for a constant ![]() ,
, ![]() gradually decreases
with the increase of
gradually decreases
with the increase of ![]() . It also shows
that the
. It also shows
that the ![]() increases with the increase of
increases with the increase of ![]() for constant
for constant ![]() showing dependency on
showing dependency on ![]() .
.
3. 4. Effect of Channel Diameter on Water-side Pressure Drop
In a
minichannel heat exchanger (![]() ), pressure drop is one
of the most important factors governing the heat exchanger performances. The
overall pressure drop in the
), pressure drop is one
of the most important factors governing the heat exchanger performances. The
overall pressure drop in the ![]() usually refers to the
sum of pressure drop in the manifolds, the straight flow path, and the
serpentine. It strongly depends on the geometric parameters of the device,
especially hydraulic diameter of the channel. The overall pressure drop of
water,
usually refers to the
sum of pressure drop in the manifolds, the straight flow path, and the
serpentine. It strongly depends on the geometric parameters of the device,
especially hydraulic diameter of the channel. The overall pressure drop of
water, ![]() , inside the
, inside the ![]() channels is reported in
Figures 5a and 5b. From Figure 5a, it is evident that
channels is reported in
Figures 5a and 5b. From Figure 5a, it is evident that ![]() increases with the
decrease of channel diameter in a power law trend. For a constant Reynolds
number of 100, the
increases with the
decrease of channel diameter in a power law trend. For a constant Reynolds
number of 100, the ![]() in 0.25 mm diameter
channel is about 54 times higher than that of 1.00 mm channel; whereas, it is
found to be 27 times higher for
in 0.25 mm diameter
channel is about 54 times higher than that of 1.00 mm channel; whereas, it is
found to be 27 times higher for ![]() . From the figure, it is
obvious that the changes in pressure drop are higher for smaller channel
diameter of 0.25 mm and lower Reynolds number of 100. The differences in
. From the figure, it is
obvious that the changes in pressure drop are higher for smaller channel
diameter of 0.25 mm and lower Reynolds number of 100. The differences in ![]() gradually decreases
with decreasing Reynolds number and increasing channel diameter; it becomes
negligible at channel diameter,
gradually decreases
with decreasing Reynolds number and increasing channel diameter; it becomes
negligible at channel diameter, ![]() for all Reynolds number
ranging from 100 to 1300.
for all Reynolds number
ranging from 100 to 1300.
As
expected, Figure 5b shows that the ![]() increases rapidly with
increase of
increases rapidly with
increase of ![]() which follows a power
law trend.
which follows a power
law trend.
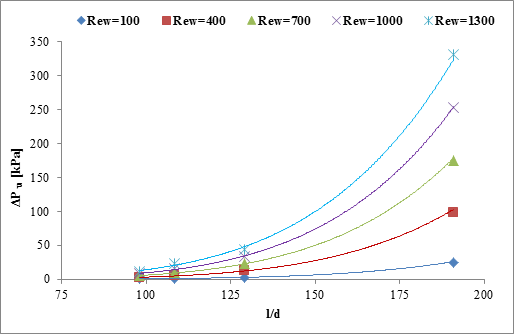
 on water-side pressure
drop for different
on water-side pressure
drop for different 
4. Conclusion
The effect of circular channel diameter on heat transfer and pressure drop through thin slabs of multiport serpentine minichannel heat exchanger for De-ionized water is studied numerically. The following conclusions are made based on the results computed from numerical simulations:
-
1- For the investigation range and a constant
 ,
, 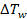 is higher with higher
is higher with higher 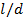 , and for a
constant
, and for a
constant 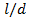 ,
, 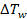 increases with the decrease of
increases with the decrease of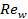 .
. -
2- For a constant
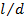 , the heat transfer coefficient (
, the heat transfer coefficient (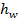 ) is higher with a higher
Reynolds number (
) is higher with a higher
Reynolds number (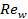 ) in a laminar flow
regime. For a constant
) in a laminar flow
regime. For a constant 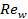 ,
, 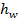 also increases
with the increase of
also increases
with the increase of 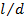 .
. -
3- The pressure drop,
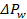 in 0.25
in 0.25 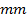 channel is almost 54
times higher than that of 1.00
channel is almost 54
times higher than that of 1.00 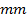 channel for
channel for 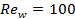 and about 27 times
higher for
and about 27 times
higher for 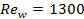 .
. - 4- The variation in the pressure drop is higher for smaller channel diameter and higher Reynolds number; it is almost diminishes at higher diameter of 1 mm for all Reynolds number ranging from 100 to 1300.
- 5- The
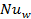 is higher with both the
higher
is higher with both the
higher 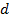 for a constant
for a constant 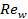 , and with the higher
, and with the higher 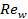 for a constant
for a constant 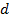 . However,
. However, 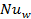 has a faster gradient
at the smaller
has a faster gradient
at the smaller 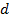 .
. - 6- The
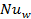 is higher with higher
is higher with higher 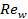 at a constant
at a constant 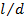 showing
dependency on
showing
dependency on 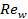 . Inversely, the
. Inversely, the 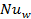 is lower at a higher
is lower at a higher 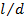 at constant
at constant 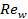 .
. - 7- Even though it is
observed that for Reynolds number of 100, Nusselt number becomes close to 3.66
regardless of channel diameter, a higher
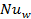 is observed for all cases considered in
the current study than in the theoretical prediction for fully
developed laminar flow circular tubes. The reason is that the current flow is a
developing flow along the channel.
is observed for all cases considered in
the current study than in the theoretical prediction for fully
developed laminar flow circular tubes. The reason is that the current flow is a
developing flow along the channel.
Acknowledgement
The authors are grateful to the Natural Sciences and Engineering Research Council of Canada
(NSERC) and the University of Windsor, Canada for financial support for the research.
References
[1] B.X. Wang, X.F. Peng "Experimental investigation of liquid forced-convection heat transfer through microchannels", International Journal of Heat Mass Transfer, 37, 1994, 73–82. View Article
[2] F.W. Dittus, L.M.K. Boelter "Heat transfer in automobile radiators of the tubular type" University of California Publications in Engineering, 2, 1930 443-461. View Book
[3] R.L. Webb, M. Zhang "Heat transfer and friction in small diameter channels" Micro scale Thermophysics Engineering, 2, 1998, 189- 202. View Article
[4] P.Y. Wu, W.A. Little "Measurement of the heat transfer characteristics of gas flow in fine channel heat exchangers used for microminiature refrigerators" Cryogenics, 24, 1984, 415–420. View Article
[5] I. Papautsky, T. Ameel, A.B. Frazier "A review of laminar single-phase flow in microchannels" Micro-Electro-Mechanical Systems (MEMS). 2001 ASME International Mechanical Engineering Congress and Exposition, 2001, p 495-503. View Article
[6] B. Agostini, A. Bontemps, B. Thonon "Effects of geometrical and thermophysical parameters on heat transfer measurements in small diameter channels" Heat Transfer Engineering, 27, 2006, 14-24. View Article
[7] V. Gnielinski "New equation for heat and mass transfer in turbulent pipe and channel flow" International Journal of Chemical Engineering, 16, 1976, 359-368.
[8] Z. Li, Y-L. He, G-H. Tang, W-Q. Tao "Experimental and numerical studies of liquid flow and heat transfer in microtubes" International Journal of Heat and Mass Transfer, 50, 2007, 3447–3460. View Article
[9] T. Harirchian, S.V. Garimella "Effects of channel dimension, heat flux, and mass flux on flow boiling regimes in microchannels" International Journal of Multiphase Flow. 35, 2009, 349–362. View Article
[10] Z.Y. Guo, Z.X. Li "Size effect on micro scale single-phase flow and heat transfer" International Journal of Heat and Mass Transfer. 46, 2003, 149–159. View Article
[11] G.M. Mala, D. Li "Flow characteristics of water in microtubes" International Journal of Heat Fluid Flow, 20, 1999, 142-148. View Article
[12] D. Lelea, S. Nishio, K. Yakano "The experimental research on microtube heat transfer and fluid flow of distilled water" International Journal of Heat and Mass Transfer, 47, 2004, 2817-2830. View Article
[13] M. Venkatesan, S.K. Das, A.R. Balakrishnan "Effect of diameter on two-phase pressure drop in narrow tubes" Experimental Thermal and Fluid Science, 35, 2011, 531–541. View Article
[14] S.G. Kandlikar "Two-Phase Flow Patterns, Pressure Drop, and Heat Transfer during Boiling in Minichannel Flow Passages of Compact Evaporators" Heat Transfer Engineering 23, 2002, 5–23. View Article
[15] M. Ismail, A. Fartaj, M. Karimi "Numerical investigation on heat transfer and fluid flow behaviors of viscous fluids in minichannel heat exchanger" Numerical Heat Transfer, Part A: Applications, 64, 2013, 1-29. View Article
[16] M.G. Khan and A. Fartaj "A Review on Microchannel Heat Exchangers and Potential Applications" International Journal of Energy Research, 35(7), 2011, 553–582. View Article
[17] Y.A. Cengel "Heat Transfer, a Practical Approach", 4th edition. McGraw-Hill, 2007.