International Journal of Mechanical Engineering and Mechatronics (IJMEM)

ISSN: 1929-2724

1. Introduction

The target of the manufacturing enterprise is to provide the best product at a lower price and with the lowest operating cost. Cost must be reduced without sacrificing the technical superiority of products [1]. The manufacturing processes of fasteners generally include wire-manufacturing, forming, heat treating, coating, and packing. Many well-developed fastener products, for cost reduction and work division, are usually fabricated by various subcontract factories, such as wire-manufacturers, forming factories, heat treating factories, and coating factories. The tapping screw, as shown in Figure 1, is a well-developed, widely used fastener. The manufacturing processes of tapping screws are sequentially wire-manufacturing, forming (heading and threading), carburizing heat treatment, and phosphate coating, which can be conducted by subcontract factories.

For wire-manufacturing, a cold-heading-quality alloy steel rod is used to manufacture wire for cold heading. Generally, the wire made from the quality rod is spheroidizing annealed, either in a single process or after drawing the finished product [2]. The wire is produced by drawing wire coil into wire, followed by heat treatment, cleaning and coating, and a final drawing operation for cold forming. Spheroidizing provides the needed ductility for cold heading [3]. Spheroidization of cementite lamellae through spheroidize annealing improve the ductility of steel [4]-[6]. Most wire-manufacturers use subcritical process for spheroidized annealing. The quality of wire-manufacturing affects the forming quality of screws. Taguchi method may be used to obtain the optimum quality of low carbon steel wire [7]. However, excessive composition of titanium may seriously affect the formability of steel wire [8].

For forming process, cold forging is often applied in the fastener industry. Cold forging is performed at room temperature and is used to achieve better tolerance, higher mechanical properties, and a better surface aspect that can avoid further machining [9]. Cold heading is a forming process of increasing the sectional area of a billet at one or more points along its length. Along with the heading process, cold-headed parts may also undergo thread rolling [2]. The level of quality is due to the well mechanical properties of cold-headed parts, an uninterrupted fiber flow, close tolerances and a good surface quality. The cost benefit achieved using forging techniques is considerable.

In order to readily fabricate into tapping screws, low-carbon steel wire is usually used. To increase the strength of screws in self-drilling operation, a case-hardening treatment is usually an essential process. Gas carburizing is a case-hardening process in which carbon is dissolved in the surface layers of a low-carbon steel part at a temperature sufficient to render the steel austenitic, followed by quenching and tempering to form a martensitic microstructure [10]. The carburizing temperature varies from 870 to 940 °C the gas atmosphere for carburizing is produced from liquid or gaseous hydrocarbons such as propane, butane or methane [11]. The process converts the outer layer of a screw into high-carbon steel, with a content range of 0.9-1.2% carbon. The resulting gradient in carbon content below the surface of the screws causes a gradient in hardness, producing a strong, wear-resistant surface layer on the material. The successful operation of the gas carburizing process depends on the control of various principal variables, such as temperature, time and atmosphere composition, which is usually conducted in a continuous carburizing furnace. Ivanov et al. [12] studied carburizing and different heat treatments of low-carbon martensitic steel 24Kh2G2NMFB and suggested heat treatment modes improving the structure of the surface layer after carburizing. Yang and Liu [13] study the effects of case-treating parameters affected on the quality of AISI 1016 self-drilling tapping screws by using Taguchi method.

Phosphating is a widely used method of reducing wear on machine elements [14]. Zinc phosphate is usually used to treat forged steel screws to increase wear resistance and corrosion protection. Screws are coated in tumbling barrels immersed in phosphating solution. Coatings can be produced with a wide range of thicknesses, depending on the method of cleaning before treatment, composition of the phosphating solution, temperature, and duration of treatment.

The manufacturing qualities of subcontract factories are sometimes uneven and resulting in difference in quality of products, even producing poor-quality products. Therefore, it is important to evaluate the subcontract factories. Taguchi method is a quality improvement technique that uses experimental design methods for efficient characterization of a product or process, combined with a statistical analysis of its variability with the fact that pre-production experiments, properly designed and analysed, can significantly contribute to efforts towards the accurate characterization and optimization of industrial processes, the quality improvement of products, and the reduction of costs and waste [15]. In this study, to improve the quality of tapping screws, Taguchi method is used to evaluate the manufacturing qualities of subcontract factories.

2. Experiment Design

AISI 1018 low carbon steel tapping screws are investigated in this study. Four manufacturing processes with three subcontract factories listed in Table 1 are selected as the experimental factors. Every process has three subcontract factories to evaluate the manufacturing qualities of tapping screws.

Table 1. Experimental factors and their subcontract factories for L₉ orthogonal array.

Factor (process)	Subcontract factory
W: Wire manufacture	W1	W2	W3
F: Forming process	F1	F2	F3
H: Heat treatment	H1	H2	H3
C: Coating process	C1	C2	C3

Taguchi method allows the changing of many factors at the same time in a systematic way, ensuring the reliable and independent study of the factors’ effects. The orthogonal array table, L₉(3⁴), is used as an experimental design for these four factors [16], as listed in Table 2.

Table 2. L₉(3⁴) orthogonal array experimental parameter assignment.

Exp. No.	Subcontract factory
	W:Wire manufacture	F:Forming process	H:Heat treatment	C:Coating process
L1	W1	F1	H1	C1
L2	W1	F2	H2	C2
L3	W1	F3	H3	C3
L4	W2	F1	H2	C3
L5	W2	F2	H3	C1
L6	W2	F3	H1	C2
L7	W3	F1	H3	C2
L8	W3	F2	H1	C3
L9	W3	F3	H2	C1

Process capability is a measure of the nature behaviour of the process after special causes of variation are eliminated, and the basic purpose is to compare the “normal variation” of the process against the design tolerances to assess whether the process can meet those specifications [1].

In this study, the quality characteristics of tapping screws, such as case hardness, core hardness, torsional strength, and drilling time, are investigated, and so are their process capabilities. As assigned by the company, the case hardness of a tapping screw is tested by a Vickers procedure with a specified range of 600-800 HV and the core hardness is with a specified range of 300-500 HV. The minimum torsional strength of a tapping screw is 2.84 N×m.

For the case/core hardness of tapping screws, the process capability is measured as [1]

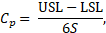
where USL is the upper specification limit, LSL is the lower specification limit and S is the process standard deviation of each trial. For the torsional strength of tapping screws, when only lower specification limit is necessary, the process-capability ratio [1] is measured,

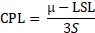where μ is the process average of each trial.

The most important quality characteristic of a tapping screw is the drilling performance, which is the ability of a screw to penetrate a piece of galvanised steel under controlled force and speed is measured. The tapping screw shall be, under controlled force of 12kg, penetrated a thickness of 0.7 mm steel plate not exceeding 1 second, which is assigned by the company. When only upper specification limit is necessary, the process-capability ratio [1] is measured.

Each test trial, including 10 specimens, is followed by each fabrication process and the results are then transformed to the S/N ratio (signal-to-noise ratio). In terms of the desired characteristics for drilling time, the shorter the better, and the S/N ratio is [16]

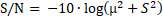where μ is the mean of each trial and S is the standard deviation.

Analysis of variance (ANOVA) is an effective method to determine the significant factors and the optimal subcontract factories to obtain optimal quality. For Taguchi method, the experimental error is evaluated with ANOVA to carry out the significance test of the various factors. The nature of the interaction between factors is considered as experimental error [16]. If the effect of a factor in comparison to the experimental error is sufficiently large, it is identified as a significant factor.

3. Results and Discussion

The experiment results of case hardness, core hardness, torsional strength and drilling time (mean, μ; standard deviation, S; process-capability ratio; and S/N ratio) are shown in Tables 3 and 4. The means of case hardness vary from 664.6 to 727.2 HV, which are all within the specified range of 600-800 HV. The standard deviation of test L6 is the smallest of the nine tests, while the standard deviation of test L4 is the largest. The process-capability ratio of test L4, C_p = 0.78, is smaller than 1, which means that the natural variation of the process (6S) is much larger than the tolerance band given.

For core hardness, the means vary from 419.0 to 468.6 HV, which are all within the specified range of 300-500 HV also. The standard deviations of tests L6 and L8 are respectively the smallest and the greatest. The process-capability ratios of all nine tests are larger than 1, which mean that the natural variations of the process (6S) are smaller than the tolerance band given. For torsional strength, the means of all nine tests are greater than the specified value (> 2.84 N ×m), as shown in Table 3, and all the process-capability ratios are also larger than 2, that is, the natural variations of the process are much smaller than the tolerance band given. These quality characteristics of tapping screws meet the requirement of specification.

Table 3. The experimental results for hardness and torsional strength.

Exp. No.*	Case hardness			Core hardness			Torsional strength
	m(HV)	S	Cp	m(HV)	S	Cp	m (N×m)	S	CPL
L1	671.4	20.7	1.61	441.8	21.4	1.55	3.85	0.128	2.61
L2	664.6	27.6	1.21	442.4	13.7	2.43	3.92	0.000	-
L3	717.0	18.7	1.78	445.0	15.7	2.13	3.96	0.088	4.25
L4	695.2	42.8	0.78	419.0	19.1	1.74	3.67	0.088	3.13
L5	722.4	12.2	2.72	441.4	17.3	1.93	3.75	0.082	3.67
L6	693.8	7.8	4.30	468.6	5.5	6.06	4.00	0.082	4.70
L7	727.2	12.5	2.66	420.4	23.3	1.43	3.92	0.000	-
L8	680.8	13.6	2.46	441.2	23.5	1.42	3.77	0.054	5.72
L9	666.2	14.3	2.34	437.6	5.6	5.96	3.75	0.082	3.67
Ave.	693.2	18.9	2.21	439.7	16.1	2.74	3.84	0.067	-

*Experimental conditions as defined in Table 2.

Table 4. The experimental results for drilling time.

Exp.No.	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	m(sec)	S	S/N ratio	CPU
L1	2.0	1.1	1.0	0.9	1.3	1.1	0.9	1.1	0.9	0.9	1.12	0.34	-1.36	-0.12
L2	1.2	0.9	0.9	0.9	0.9	0.9	0.8	0.8	1.0	0.8	0.91	0.12	0.74	0.25
L3	0.8	0.9	1.1	0.7	0.9	0.9	0.8	0.8	0.8	0.8	0.85	0.11	1.34	0.46
L4	0.9	1.0	0.9	0.9	1.0	0.9	1.0	1.0	1.1	0.9	0.96	0.07	0.33	0.19
L5	0.9	0.8	1.0	0.9	0.9	0.7	0.8	0.8	0.9	1.1	0.88	0.11	1.04	0.35
L6	0.8	0.8	1.0	0.9	0.8	0.7	0.7	0.8	0.9	0.8	0.82	0.09	1.67	0.65
L7	0.7	0.7	0.7	0.8	0.7	0.7	0.8	0.8	1.0	0.7	0.76	0.10	2.31	0.83
L8	0.9	0.8	0.9	1.0	1.0	0.8	0.9	0.8	0.8	0.9	0.88	0.08	1.08	0.51
L9	1.3	2.3	1.0	1.4	0.8	2.5	1.5	2.8	1.4	1.7	1.67	0.66	-5.08	-0.34
										Ave.	0.98	0.19	0.23	0.31

*Experimental conditions as defined in Table 2.

However, for the drilling performance test, the means of drilling time for tests L1 and L9 are exceeding 1 sec, as shown in Table 4, which do not meet the specification. Especially for test L9, the mean drilling time of 1.670 sec is too much, its standard deviation is the greatest and the S/N ratio is the smallest of the nine tests. Furthermore, the process-capability ratios of all nine tests are much smaller than 1. The natural variations of the process are much larger than the tolerance band given. The performance qualities of tapping screws are obviously affected by the manufacturing qualities of subcontract factories.

3. 1. Drilling Time

To obtain optimum quality, analysis of variance (ANOVA) is an effective method to determine significant factors and optimum subcontract factories. The contribution of each factor constructed in Table 5 could identify the significant factor affecting the performance quality of tapping screws.

Table 5. Variance analysis table of S/N ratios for drilling time.

Factor	SS	DOF	Var.	Contribution
W (Wire manufacture)	3.73	2	1.86	9.3%
F (Forming process)	4.22	2	2.11	10.6%
H (Heat treatment)	12.85	2	6.42	32.1%
C (Coating process)	19.21	2	9.60	48.0%
Total	40.00	8	-	100.0%

SS: sum of square; DOF: degree of freedom; Var.: variance.

The contribution of a factor is the percentage of the sum of squares (SS), that is, the percentage of the factor variance to the total quality loss [15]-[16]. It is clear from the ANOVA table that the contribution of coating process (C) is 48.0% of the total variation, which is the highest contributor to the variability of the experimental results. The contribution of heat treating process (H) is 32.1%, which is the second highest contribution. However, the factors of the forming process (F) and wire manufacture (W) are not significant for the S/N ratio because their contributions are relatively small.

Figure 2 illustrates the factor response diagram and the level averages of four factors with respect to the S/N ratio for drilling time. For each factor, the effect is the range of the level averages and the maximum level average is the optimum level [15]-[16]. For the significant factors of coating process (C) and heat treatment (H), subcontract factory C2 for the coating process and subcontract factory H3 for the heat treatment are evidently the optimum subcontract factories, as shown in Figure 2. The effects of the other two processes, the forming process (F) and the wire process (W), are relatively small since they are well-developed manufacturing processes for tapping screws. The optimum subcontract factories are F2 for the forming process and W2 for the wire process, respectively.

3.2. Confirmatory Experiments

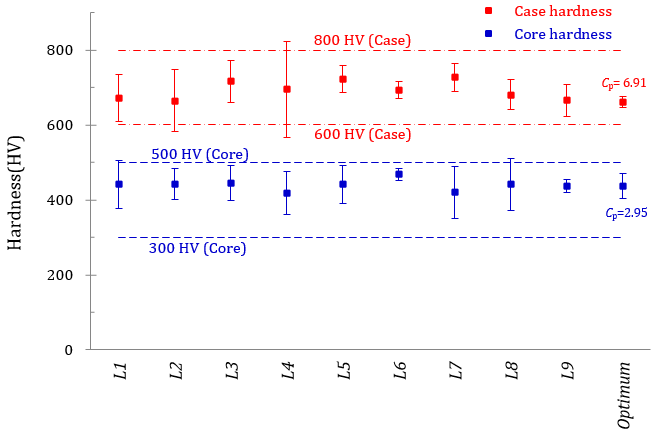
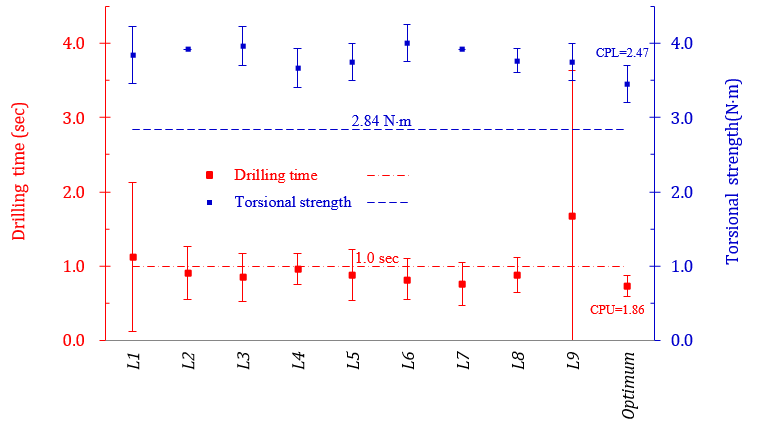
In order to verify the predicted results, tapping screws are fabricated with the optimum subcontract factories: W2, F2, H3 and C2 (as described in Figure 2). Variation is the inability to perform a task consistently according to a specification [1]. Figure 3 shows the natural variation of the process (6 process standard deviations, 6S [1]) of the nine tests and confirmatory experiment (optimum), including the given specification spans, for the case and core hardness of tapping screws; and Figure 4 is shown for the torsional strength together with drilling time of tapping screws, also including the given specification limits.

Compared with the results of the nine tests, the optimum mean case hardness of 662.4 HV is smaller than the mean value (693.2 HV in Table 3), the natural variation of the process (6S) is obviously decreased and much smaller than the given tolerance band, as shown in Figure 3, and so the optimum process-capability ratio, C_p = 6.91, is much larger than 1. The optimum mean core hardness of 437.8 HV is decreased as well compared to the average (439.7 HV in Table 3) and the natural variation of the process (6S) is also much smaller than the given tolerance band, as shown in Figure 3, and so the optimum process-capability ratio, C_p = 2.95, is larger than 1. This means that the process is capable of ensuring 99.73% of good products in hardness [1].

For the torsional strength, as shown in Figure 4, the mean values of the nine tests are much greater than the lower specification limit. However, the optimum mean torsional strength of 3.45 N×m is smaller than the average (3.84 N×m in Table 3), and the natural variation of the process is still larger than the lower specification limit, as shown in Figure 4, and so the optimum process-capability ratio, CPL = 2.47, is much larger than 1.

Although the three quality characteristics of tapping screws almost meet the requirement of specification for the nine tests, the drilling performance is not good enough, as shown in Figure 4, because all the natural variations of the process are exceeding the upper specification limit for the drilling time; and their process-capability ratios, CPU as shown in Table 4, are all smaller than 1. This means that the natural variations of the process are much larger than the specification limit given. Thus, the process is incapable of ensuring 99.73% of good tapping screws [1].

However, the optimum mean drilling time of 0.73 sec is not only smaller than the average (0.98 sec in Table 4); but also the optimum process-capability ratios, CPU = 1.86, is larger than 1, as shown in Figure 4. The natural variation of the process is obviously decreased and much smaller than the upper specification limit. Therefore, with the optimum subcontract factories: W2, F2, H3 and C2, the process is capable of ensuring 99.73% of good tapping screws. That is, guarantee that only 2700 ppm is expected to be defective.

4. Conclusion

The tapping screw is a well-developed, widely used fastener. The manufacturing processes of tapping screws are sequentially wire-manufacturing, forming (heading and threading), carburizing heat treatment, and phosphate coating, which can be conducted by subcontract factories. The manufacturing qualities of subcontract factories are sometimes uneven and resulting in difference in quality of products. The performance qualities of tapping screws are affected by the manufacturing qualities of subcontract factories. In this study, to improve the quality of AISI 1018 low carbon steel tapping screws, Taguchi method is used to evaluate the manufacturing qualities of subcontract factories. The quality characteristics of tapping screws, such as case hardness, core hardness, torsional strength, and drilling time, are investigated. The most important quality characteristic of a tapping screw is the drilling performance.

It is experimentally revealed that the heat treating process (H) and the coating process (C) are the significant processes; while the forming process (F) and the wire process (W) are relatively not significant since they are well-developed manufacturing processes for tapping screws, which may be used to achieve the cost benefit. The determined subcontract factories are factory H3 for the heat treating process, factory C2 for the coating process, factory F2 for the forming process, and W2 for the wire process. In addition, the optimum drilling performance is 0.73 sec mean drilling time which is not only much smaller than the upper specification limit, but also the optimum process-capability ratios, CPU = 1.86, is larger than 1. Therefore, the process is capable of ensuring 99.73% of good tapping screws. The determined subcontract factories: W2, F2, H3 together with C2, evidently improve the performance measures. The drilling performance of the AISI 1018 tapping screws is effectively improved.

Acknowledgements

The authors would like to acknowledge the support of TYCOONS Group Enterprise Co., Ltd., Kaohsiung, Taiwan, for providing the materials and apparatus to carry out the experimental works.

References